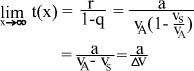Achill und die Schildkröte

Obwohl die Schildkröte langsamer ist als der Läufer Achill, kann sie nicht von ihm eingeholt werden, wenn sie einen kleinen Vorsprung hat. Achill müsste zuerst an den Punkt kommen, an dem die Schildkröte gestartet ist. Bis dahin ist die Schildkröte aber schon weitergelaufen. Achill muss wieder an den Punkt, an dem die Schildkröte war, die jedoch wieder ein Stück weitergelaufen ist. Das können sie nun unendlich weitermachen, und Achill wird die Schildkröte nie einholen. (Zenon von Elea)



Dieser Beweis ist offensichtlich falsch. Nach ein wenig Nachdenken kommt man schnell darauf, dass es daran liegen könnte, dass das Einholen immer kürzer dauert, und die Gesamtzeit somit einen bestimmten Wert nicht überschreitet. (Zum Beispiel ist 1 + 1/2 + 1/4 + 1/8 + 1/16... immer kleiner als 2.)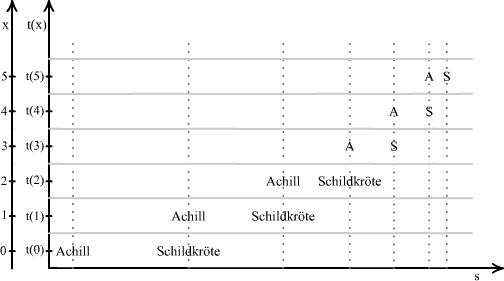

Diese Vermutung gilt es nun zu beweisen:

Zuerst wollen wir eine Funktion aufstellen, die den Zeitpunkt für jedes Erreichen des ehemaligen Schildkrötenaufenthaltsplatzes definiert. Die Funktion sei t(x), wobei x die Anzahl der Läufe von Achill ist. (Achill und die Schildkröte machen zwischen den Läufen keine Pausen.)
Nach 0 Läufen ist die vergangene Zeit auch 0, also t(0)=0.


Nun kann man eine Formel aufstellen:

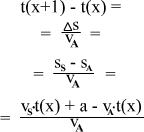
t(x+1) - t(x) = Δs/v_A = (s_S - s_A)/v_A = (v_S·t(x) - v_A·t(x))/v_A

t(x+1)-t(x) ist die Zeit, die Achill benötigt, um die Strecke Δs zu laufen.

Δs ist der Abstand zwischen Achill und der Schildkröte im x-ten Lauf.

vA ist die Geschwindigkeit von Achill.

sS ist der Ort von der Schildkröte im x-ten Lauf.

sA ist der Ort von Achill im x-ten Lauf.

vS ist die Geschwindigkeit der Schildkröte.

a ist der Vorsprung der Schildkröte.


Die Formel wird nach t(x+1) aufgelöst und vereinfacht: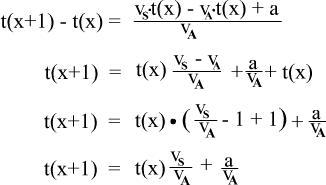

t(x+1) - t(x) = (v_S·t(x) - v_A·t(x) + a)/v_A  =>  t(x+1) = t(x)·(v_S - v_A)/v_A + a/v_A + t(x)  =>  t(x+1) = t(x)·(v_S/v_A - 1 + 1) + a/v_A  =>  t(x+1) = t(x)*v_S/v_A + a/v_A

vS, vA und a sind gegeben. Nun wird substituiert:

q := vS/vA

r := a/vA


Die Gleichung heißt nun:

t(x+1) = t(x)·q + r

Das ist die Formel der nachschüssigen(postnumeranden) Ratenzahlung mit Zinsen. Gelöst wird die Gleichung durch

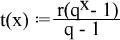
t(x) := r(q^x - 1)/(q-1)

Dies lässt sich durch Einsetzen beweisen:

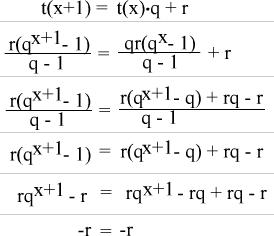
t(x+1) = t(x)·q + r  =>  r(q^(x+1) - 1)/(q-1) = qr(q^x-1 - 1)/(q-1) + r  =>  r(q^(x+1) - 1)/(q-1) = (r(q^(x+1) - q) + rq - r)/(q-1)  =>  r(q^(x+1) - 1) = r(q^(x+1) - q) + rq - r  =>  rq^(x+1) - r = rq^(x+1) - rq + rq - r  =>  -r = -r

Da eine wahre Aussage herauskommt, löst diese Formel die Gleichung.
Um nun auszurechnen, ob die Gesamtzeit nach unendlich vielen Schritten einen bestimmten Wert nicht überschreitet, benutzen wir den Grenzwert:

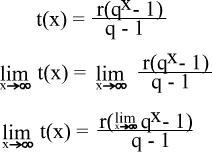
t(x) = r(q^x - 1)/(q-1)  =>  lim_x->oo t(x) = lim_x->oo r(q^x - 1)/(q-1)  =>  lim_x->oo t(x) = r(lim_x->oo q^x - 1)/(q-1)

Aus q=vS/vA und vS<vA folgt q<1. Somit gilt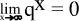

lim_x->oo q^x = 0

Das wird in die obige Formel eingesetzt und man kommt zum Ergebnis:

lim_x->oo t(x) = r(0-1)/(q-1)  =>  lim_x->oo t(x) = -r/(q-1)  =>  lim_x->oo t(x) = r/(1-q)

Die benötigte Zeit ist also offensichtlich nicht unendlich. Vielmehr lässt sich durch diese Formel die Zeit, die zum Einholen benötigt wird, ausrechnen. Dazu werden einfach r und q eingesetzt:

lim_x->oo t(x) = r/(1-q) = a/(v_A(1-v_S/v_A)) = a/(v_A/v_S) = a/Δv

Man erhält also am Ende wieder die normale Formel zur Berechnung der benötigten Zeit.