Wie man mit den Fingern addieren kann, weiß wohl jeder. Es gibt aber auch mehr oder weniger einfache Verfahren zur Multiplikation mit den Fingern. Bauern aus der Auvergne kannten schon ein Verfahren, um zwei Zahlen von 5 bis 10 mit Hilfe der Hände miteinander malzunehmen. Dabei vertritt jede Hand eine Zahl. Die Hände werden folgendermaßen durchnummeriert:
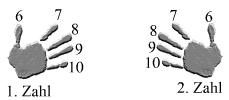
Nun zieht man alle Finger nach dem Faktor ein. Wenn man z.B. 7

9 rechnen will, schaut das so aus:
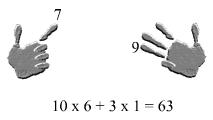
Die Zahl lässt sich dann nach dieser Regel errechnen:
10  Ausgestreckte Finger insgesamt + ( Eingezogene Finger links
Ausgestreckte Finger insgesamt + ( Eingezogene Finger links  Eingezogene Finger rechts )
Eingezogene Finger rechts )
Wie man am Beispiel sieht, funktioniert das auch. Es folgt der
a sei die erste Zahl und b die zweite Zahl von 5 bis 10. Da jede Hand mit 6 beginnt, sind die ausgestreckten Finger
a-5 und
b-5. Die Anzahl der insgesamt ausgestreckten Finger ist also
a-5 + b-5 = a+b - 10. Die Anzahl der eingezogenen Finger erhält man, wenn man die ausgestreckten Finger von der Anzahl der Finger einer Hand abzieht:
Eingezogene Finger links:
5 - (a-5) = 10-a
Eingezogene Finger rechts:
5 - (b-5) = 10-b
Nun kann man einsetzen:
10  Ausgestreckte Finger insgesamt + Eingezogene Finger links
Ausgestreckte Finger insgesamt + Eingezogene Finger links  Eingezogene Finger rechts =
Eingezogene Finger rechts =
= 10(a + b - 10) + (10-a)(10-b) =
= 10a + 10b - 100 + 100 - 10b - 10a +ab =
= ab
Also funktioniert das Verfahren.
(Wer nur an den Regeln für höhere Zahlen interessiert ist, und nicht wie man darauf kommt, kann
hier klicken.)
Man kann nun weitere solche Regeln erfinden. Wenn man eine Regel für zwei Zahlen von
x bis
x+5 haben will, und der erste Faktor a und der zweite Faktor b ist, sind an der ersten Hand
a-x Finger und an der zweiten
b-x Finger ausgestreckt.
Wie man an den obigen Formeln erkennt, muss man immer einen festen Summanden und die mit einem festen Faktor malgenommene Summe der ausgestreckten Finger mit dem Produkt entweder der ausgestreckten Finger jeder Hand oder der eingezogenen Finger jeder Hand zusammenzählen. Das lässt sich so in Formeln fassen:
(1) s + f(a-x + b-x) + (a-x)(b-x)
oder
(2) s + f(a-x + b-x) + ( 5-(a-x) )( 5-(b-x) )
Allgemeine Regel für (1)
Vereinfachung:
s + f(a-x + b-x) + (a-x)(b-x) =
= s + f(a+b-2x) + ab - xa - xb + x2 =
= s + fa + fb - 2fx + ab - xa - xb + x2
Dass man eine funktionierende Fingermultiplikationsregel bekommt, darf nur noch
ab ürigbleiben, d.h
s+fa+fb-2fx-xa-xb+x2 muss 0 sein. Dazu ist es vorteilhaft, wenn man f:=x setzt. Nun wird der Term
fa+fb-xa-xb=0. Übrig bleibt
s - 2fx + x2 + ab =
= s - 2x2 + x2 + ab =
= s - x2 + ab
Nun soll
s-x2=0 sein. Das ist eine Gleichung die man auf s auflösen kann:
s - x2 = 0
s = x2
Da x gegeben ist, sind nun auch f (
f=x) und s (
s=x2) errechenbar, man kann also verallgemeinern:
Für zwei Zahlen a und b von
x bis
x+5 gilt folgende Regel:
x2 + x  Ausgestreckte Finger insgesamt + Ausgestreckte Finger links
Ausgestreckte Finger insgesamt + Ausgestreckte Finger links  Ausgestreckte Finger rechts
Ausgestreckte Finger rechts
Die Durchnummerierung ist dabei so, dass die Daumen jeweils x sind und die kleinen Finger x+5.
Allgemeine Regel für (2)
Zuerst wird vereinfacht:
s + f(a-x + b-x) + ( 5-(a-x) )( 5-(b-x) ) =
= s + fa + fb - 2fx + ( (5+x)-a )( (5+x)-b ) =
= s + fa + fb - 2fx + (5+x)2 - (5+x)a - (5+x)b + ab
Hier ist es sinnvoll,
f:=5+x zu setzen, da dann der Term
fa+fb-(5+x)a-(5+x)b wegfällt. Es bleibt also:
s - 2fx + (5+x)2 + ab =
= s - 2(5+x)x + (5+x)2 + ab =
= s - 10x - 2x2 + 25 + 10x + x2 + ab =
= s - x2 + 25 + ab
Hier soll auch
s-x2+25=0 sein. Jetzt wird wieder nach s aufgelöst:
s - x2 + 25 = 0
s = x2 - 25
Die allgemeine Regel ist also:
(x2 - 25) + (5+x)  Ausgestreckte Finger insgesamt + Eingezogene Finger links
Ausgestreckte Finger insgesamt + Eingezogene Finger links  Eingezogene Finger rechts
Eingezogene Finger rechts
Die Durchnummerierung ist immer so wie bei (1): Daumen: x, kleine Finger: x+5.
Regel (1) funktioniert ebenso gut wie Regel (2), aber für zwei Zahlen aus dem ersten 5er eines Zehners (z.B. 13, 22, 4...) empfiehlt sich Regel (1), weil dann als Faktor immer eine Zehnerzahl herauskommt. Regel (2) nimmt man für zwei Zahlen aus einem zweiten 5er eines Zehners (z.B. 18, 26), weil durch f:=x+5 auch immer ein Zehnerfaktor herauskommt.



 9 rechnen will, schaut das so aus:
9 rechnen will, schaut das so aus:
 Ausgestreckte Finger insgesamt + ( Eingezogene Finger links
Ausgestreckte Finger insgesamt + ( Eingezogene Finger links  Eingezogene Finger rechts )
Eingezogene Finger rechts ) Ausgestreckte Finger insgesamt + Eingezogene Finger links
Ausgestreckte Finger insgesamt + Eingezogene Finger links  Eingezogene Finger rechts =
Eingezogene Finger rechts =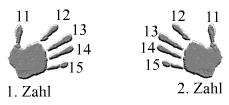
 Ausgestreckte Finger insgesamt + Ausgestreckte Finger links
Ausgestreckte Finger insgesamt + Ausgestreckte Finger links  Ausgestreckte Finger rechts
Ausgestreckte Finger rechts Ausgestreckte Finger insgesamt + Ausgestreckte Finger links
Ausgestreckte Finger insgesamt + Ausgestreckte Finger links  Ausgestreckte Finger rechts=
Ausgestreckte Finger rechts=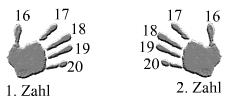
 Ausgestreckte Finger insgesamt + Eingezogene Finger links
Ausgestreckte Finger insgesamt + Eingezogene Finger links  Eingezogene Finger rechts
Eingezogene Finger rechts Ausgestreckte Finger insgesamt + Eingezogene Finger links
Ausgestreckte Finger insgesamt + Eingezogene Finger links  Eingezogene Finger rechts =
Eingezogene Finger rechts =  Ausgestreckte Finger insgesamt + Ausgestreckte Finger links
Ausgestreckte Finger insgesamt + Ausgestreckte Finger links  Ausgestreckte Finger rechts
Ausgestreckte Finger rechts
 Ausgestreckte Finger insgesamt + Eingezogene Finger links
Ausgestreckte Finger insgesamt + Eingezogene Finger links  Eingezogene Finger rechts
Eingezogene Finger rechts
 Ausgestreckte Finger insgesamt + Eingezogene Finger links
Ausgestreckte Finger insgesamt + Eingezogene Finger links  Eingezogene Finger rechts
Eingezogene Finger rechts Ausgestreckte Finger insgesamt + Ausgestreckte Finger links
Ausgestreckte Finger insgesamt + Ausgestreckte Finger links  Ausgestreckte Finger rechts
Ausgestreckte Finger rechts Ausgestreckte Finger insgesamt + Eingezogene Finger links
Ausgestreckte Finger insgesamt + Eingezogene Finger links  Eingezogene Finger rechts
Eingezogene Finger rechts Ausgestreckte Finger insgesamt + Ausgestreckte Finger links
Ausgestreckte Finger insgesamt + Ausgestreckte Finger links  Ausgestreckte Finger rechts
Ausgestreckte Finger rechts Ausgestreckte Finger insgesamt + Eingezogene Finger links
Ausgestreckte Finger insgesamt + Eingezogene Finger links  Eingezogene Finger rechts
Eingezogene Finger rechts Ausgestreckte Finger insgesamt + Ausgestreckte Finger links
Ausgestreckte Finger insgesamt + Ausgestreckte Finger links  Ausgestreckte Finger rechts
Ausgestreckte Finger rechts